PLANO INCLINADO
MARCO TEORICO
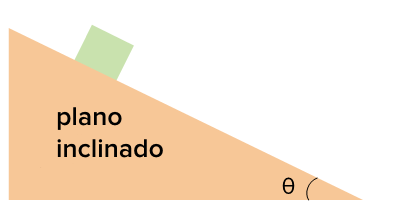
¿QUE ES UN PLANO INCLINADO ?
Las resbaladillas de los parques, los caminos empinados y las rampas de los camiones de carga son todos ejemplos de planos inclinados. Las pendientes o los planos inclinados son superficies diagonales sobre las cuales los objetos pueden estar en reposo, deslizarse o rodar hacia arriba o hacia abajo.
Los planos inclinados son útiles ya que pueden reducir la cantidad de fuerza requerida para mover un objeto verticalmente. Son considerados una de las seis máquinas clásicas simples.
¿Cómo usamos la segunda ley de Newton para lidiar con los planos inclinados?
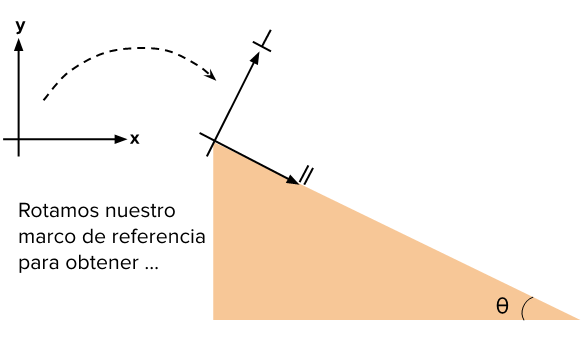
En la mayoría de los casos, resolvemos problemas que involucran fuerzas al usar la segunda ley de Newton para las direcciones vertical y horizontal. Pero para los planos inclinados, típicamente estamos preocupados con el movimiento paralelo a la superficie del plano inclinado, así que a menudo es más útil resolver la segunda ley de Newton para las direcciones paralela y perpendicular a la superficie inclinada.
Esto significa que típicamente estaremos usando la segunda ley de Newton para las direcciones perpendicular \perp y paralela \parallel a la superficie del plano inclinado.
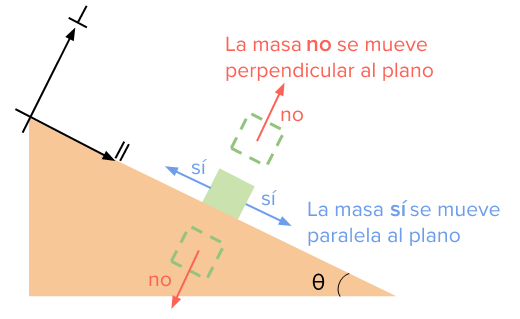
Ya que la masa a menudo se desliza paralelamente a la superficie del plano inclinado y no se mueve perpendicularmente a esta, podemos casi siempre suponer que a, start subscript, \perp, end subscript, equals, 0.
¿Cómo encontramos las componentes \perp y \parallel de la fuerza de gravedad?
Dado que estaremos usando la segunda ley de Newton para las direcciones perpendicular y paralela a la superficie del plano inclinado, vamos a necesitar las componentes de la fuerza de gravedad en estas direcciones.
Las componentes de la fuerza de gravedad se muestran en el siguiente diagrama. Ten cuidado, la gente frecuentemente se confunde al determinar si debe usar el start text, s, e, n, o, end text o el start text, c, o, s, e, n, o, end text para una componente dada.
¿Cuál es la fuerza normal F, start subscript, N, end subscript para un objeto sobre un plano inclinado?
La fuerza normal F, start subscript, N, end subscript siempre es perpendicular a la superficie que ejerce la fuerza. Así que un plano inclinado ejercerá una fuerza normal perpendicular a su superficie.
Para que no haya aceleración perpendicular a la superficie del plano inclinado, las fuerzas deben estar balanceadas en esta dirección. Si miramos el diagrama de fuerzas mostrado a continuación, vemos que para asegurar que la fuerza neta en la dirección perpendicular sea igual a cero, la fuerza normal debe ser igual a la componente perpendicular de la fuerza de gravedad.
En otras palabras, para un objeto que se encuentra ya sea en reposo o deslizándose sobre un plano inclinado,



Comentarios
Publicar un comentario